Анализ учебников Г. В. Дорофеева, Л. Г. Петерсон «Математика-5», «Математика-6» с точки зрения наличия задач для формирования умений, характерных для математического моделирования

Первоначально была изучена соответствующая теме исследования математическая и методическая литература. После чего были разработаны и проведены два занятия математического кружка по темам:

Математические модели.

Решение задач с применением метода математического моделирования.

Проведена контрольная работа по теме «Решение задач».

Подробное описание кружков и контрольной работы содержится соответственно в приложениях 1, 2, 3.

Нами были поставлены следующие цели:

познакомить учащихся с понятием математической модели;

рассмотреть основные типы задач, в которых требуется перевод условия задачи на математический язык;

выделить основные этапы моделирования;

в соответствии с этапами моделирования выделить этапы решения задач с помощью уравнений;

сравнить результаты контрольной работы в разных классах.

Занятия проводились в 6–х классах, обучающихся по учебнику [7] Н. Я. Виленкина, после изучения темы «Решение уравнений».

Занятия математического кружка проводились в 6б классе, а контрольная работа – в 6б и в 6в классах.

После проведения контрольной работы были получены следующие результаты:

1) количество человек, решивших каждую задачу в 6б больше, чем в 6в классе (см. диаграмму);

Количество человек, решивших каждую задачу

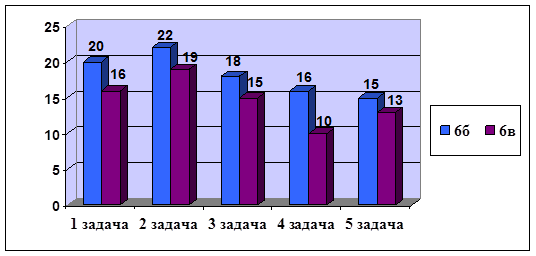
2) при решении первой задачи трудности возникли вследствие того, что в качестве переменной x многие выбрали количество автомобилей, которые отремонтировал первый механик (количество детей в младшей группе – во втором варианте), хотя целесообразно за x взять количество автомобилей, отремонтированных вторым механиком (количество детей в средней группе). Появление дробей усложнило модель задачи, и ученики не смогли решить ее. Причем в 6б правильный выбор переменной сделали на 5 человек больше, чем в 6в, этому способствовало составление таблицы к задаче.

3) при решении второй задачи в первом варианте были допущены ошибки при составлении математической модели, так как несколько человек получили не , а ;

4) в четвертой задаче большие сложности вызвали проценты, поэтому из каждого класса эту задачу смогли решить лишь 16 и 10 человек соответственно. Ребята не смогли перевести на математический язык выражения «на 60% (40%) меньше», «на 60% (40%) больше», а также у некоторых возникла сложность с выбором переменной, так в качестве переменной была выбрана искомая величина, что нецелесообразно;

5) при составлении пропорции в пятой задаче сложностей не возникло, но многие просто не успели решить ее.

Сложности при решении задач возникают в результате того, что не всегда выбор переменных являет­ся рациональным. Уже на ранних этапах обучения нужно приучать к выбору таких пе­ременных модели, которые оказываются наиболее удобными для решения задачи. Удачный выбор переменных помогает легче составить математическую модель задачи, и получить наиболее простую для реализации модель.

Также сложность вызывает перевод условия или части условия задачи на математический язык, результатом чего является неправильно построенная модель задачи.

Можно сделать вывод, что обучение действиям характерным для этапов моделирования, облегчает построение математической модели задачи, способствует построению более удобной и простой модели, и, как следствие, упрощается процесс решения задачи.

1. Анализ школьных учебников по математике для 5 – 6 классов показал, что большое внимание методу моделирования уделяется в основном в учебниках Г. В. Дорофеева, Л. В. Петерсон, в остальных учебниках или эта тема не изучается вообще, или рассматривается обзорно.

2. Учебники содержат большое количество задач, характерных для метода моделирования, а именно: задачи, непосредственно реализующие этапы процесса математического моделирования; задачи, в которых требуется выполнить действия, характерные для этапов моделирования.

Смотрите также::

Диагностика грамматического строя языка детей со стертой дизартрией
Исследование состояния сформированности грамматического строя языка является диагностическим у детей со стертой дизартрией в плане установления общего недоразвития речи. Целью исследования является установление уровня сформированности синтаксического и морфологического оформления высказывания. Пред ...

Работа с изобразительно – выразительными средствами языка
Необходимо отметить, что изобразительные средства языка метки, эмоциональны, они оживляют речь, развивают мышление, совершенствуют словарь детей. Нужно использовать все возможности в работе над изобразительными средствами языка художественных произведений: основными видами тропов (сравнением, эпите ...

Произвольное внимание как одно из центральных новообразований младшего школьного периода и другие психические функции у младшего школьника
Безусловно, учебная деятельность требует усидчивости, организации своего времени, аккуратности, ответственности и, конечно, внимания. Высокий уровень развития свойств внимания положительно влияет на успешность обучения. Тогда как у дошкольников преобладало непроизвольное внимание, естественно, перв ...