Анализ учебников Г. В. Дорофеева, Л. Г. Петерсон «Математика-5», «Математика-6» с точки зрения наличия задач для формирования умений, характерных для математического моделирования

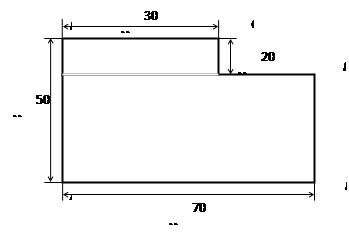
Переведи условие задачи на математический язык: Под строительную площадку отвели прямоугольный участок, длина которого на 25 м больше его ширины. При утверждении плана застройки длину участка увеличили на 5 м, а ширину – на 4 м, в результате площадь участка увеличилась на 300 м2. Какова площадь образовавшейся строительной площадки?

Построй математическую модель задачи и найди ответ методом перебора: Прямоугольный газон обнесен изгородью, длина которой 30 м. Площадь газона 56 м2. Найди длины сторон газона, если известно, что они выражаются натуральными числами.

Понятие «параллелепипед»

Прямоугольный параллелепипед является математическим эквивалентом «аквариума», «печи», «ящика», «бассейна». Например.

Из фанеры требуется сделать открытый ящик, имеющий форму прямоугольного параллелепипеда с измерениями 40 см, 20 см и 15 см. Сколько фанеры потребуется для изготовления ящика? Какова будет его вместимость?

Из жести сделали бак без крышки. Он имеет форму куба с длиной ребра 8 дм. Бак надо покрасить снаружи и изнутри. Какую площадь надо покрасить? Какова вместимость бака?

Чтобы сделать бассейн, в земле выкопали котлован в форме прямоугольного параллелепипеда длиной 25 м, шириной 6 м и глубиной 3 м. Сколько кубических метров земли пришлось вынуть?

Имеется два аквариума с измерениями 45´32´50 см и 50´32´45 см.

а) На изготовление какого из двух аквариумов потребовалось больше стекла?

б) Аквариумы заполнили водой так, что уровень воды в первом аквариуме ниже верхнего края на 10 см, а во втором – на 5 см. В каком аквариуме больше воды?

Понятия «окружность» и «круг»

При изучении окружности, круга и их свойств в учебнике используются задачи, в которых используются такие термины как «окружность колеса», «обороты колеса», «арена цирка», «циферблат часов», «беговая дорожка», «экватор Земли».

Великий древнегреческий математик Архимед (III в. до н.э.) установил, что длина окружности примерно в 3 раза больше ее диаметра. Пользуясь этим результатом, реши задачу: Какова длина беговой дорожки ипподрома, имеющей форму круга радиусом км?

Длина экватора Земли равна примерно 40000 км, а ее диаметр составляет длины экватора. Чему равен диаметр Земли?

Сколько оборотов сделает колесо на участке пути в 1,2 км, если диаметр колеса равен 0,8 м? Число p округли до целых .

Чему равна площадь циферблата часов, если длина минутной стрелки равна 4,5 см. Число p округли до целых .

Арена цирка имеет длину 40,8 м. Найди диаметр и площадь арены. Число p округли до целых (см. № 737, [15]).

Также к этой группе относятся задачи:

5 класс, часть 1, [11]: №№ 102 (3), 142 (5), 280 (1), 716, 753, 791, 800;

5 класс, часть 2, [12]: №№ 269 (5), 271 (1), 307, 352 (3), 379 (1), 380 (2);

6 класс, часть 1, [13]: №№ 56 (а);

6 класс, часть 3, [15]: №№ 341, 342, 547, 549 (2,4), 562, 566.

Также при обучении действию замены исходных терминов выбранными математическими эквивалентами применяются задачи, в которых требуется замена одной единицы измерения другой более мелкой и наоборот. Таких задач в учебниках очень много, но в основном в них требуется переводить километры в метры, метры в сантиметры, минуты в часы (№№ (5 класс, часть 1, [11]) 146 (1,2,4), 162 (2), 340 (1), 392, 406, 408, 504, 561, 581, 679, 752. 764, 786, 797, 798; №№ 44, 56, 127 (3), 221, 228, 616 (2), 769 (2), 901, 992, 1065, 1067 (5 класс, часть 2, [12]); №№ 189 (2), 190 (2), 191 (2), 198, 199, 201, 209, 210, 212, 223, 233, 247, 305, 306, 334 (6 класс, часть 1, [13]); №№ 44, 49, 125,203, 204, 292, 293 (1), 322, 372, 373, 551 (6 класс, часть 2, [14]); №№ 116, 130 (а), 132,133, 154, 195, 223, 228, 304, 433-436, 444, 465, 466, 467, 499, 563, 633, 667, 678-680, 683, 700, 706, 717, 720, 727, 728, 738, 764, 767 (б) (6 класс, часть 3, [15])), что не вызывает больших сложностей у школьников. Например.

Смотрите также::

Роль изучения элементов математического моделирования в курсе математики 5-6 классов
В литературных источниках отмечается использование моделирования в обучении математике как средства познания и осмысления нового знания, выделяются его виды, отмечаются условия, необходимые для его форми­рования (Л. М. Фридман, В. В. Давыдов, С. И. Архангельский, О. Б. Епишева, В. И. Крупич, Л. С. ...

Авторы, которые занимались изучением этой проблемы
Воспитание не является делом только педагогов и общества, воспитание и обучение детей - это дело каждой семьи, что доказывают научные труды В.М. Бехтерева, П.П. Болонского, М.И. Демкова, П.Ф. Каптерева, П.Ф. Лесгафта, М.С. Лунина, А.Н. Острогорского, А.Н. Радищева, Л.Н. Толстого, С.П. Шевырева и др ...

Некоторые теоретические подходы к определению понятия "познавательный интерес"
Проблема интереса в современной науке представлена с различных позиций. В исследованиях М.Ф. Беляева15, А.А. Невского изучается психологическая природа интереса; в работах Ю.К. Бабанского16 познавательный интерес выступает в основном как средство обучения. Познавательный интерес рассматривается В.Н ...