Анализ учебников Г. В. Дорофеева, Л. Г. Петерсон «Математика-5», «Математика-6» с точки зрения наличия задач для формирования умений, характерных для математического моделирования

Расстояние от Москвы до Бреста равно примерно 1100 км. Изобразите шоссе от Москвы до Бреста на тетрадном листе в виде отрезка, подобрав удобный масштаб (см. № 30, [14]).

В автохозяйстве для каждой модели автомобилей установлена норма износа. По «Волгам» она составляет 11,1% в год. Каков срок службы этого автомобиля? (Cм. № 434, [14]).

При решении задач на практике приходится округлять не только результат, но и исходные числовые данные. Это может происходить, например, при использовании табличных данных, где указана точность более высокая, нежели требуется по смыслу задачи. Средством обучения выбору точности исходных данных могут служить задачи:

а) требующие практических измерений;

б) связанные с чтением и построением графиков;

в) связанные с избыточной точностью числовых данных.

Задачи, требующие практических измерений

Измерь длину и ширину тетради и вырази результат в дециметрах. Вычисли площадь тетрадного листа и вырази ее в квадратных дециметрах (см. № 741, [12]).

Задачи, связанные с чтением и построением графиков

На тренировке в 50–метровом бассейне два пловца стартовали одновременно на дистанцию 200 м. Один плыл кролем, другой – брасом. На рисунке приведены графики их движения:

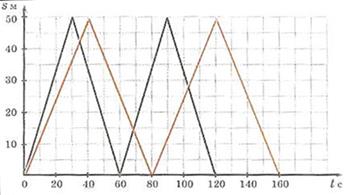
Сколько времени затратили пловцы на каждые 50 м и на всю дистанцию?

Сколько раз и на каком расстоянии от стартовой стенки бассейна встречались пловцы?

С какой скоростью плыл каждый из спортсменов?

На сколько секунд раньше финишировал первый пловец?

На сколько метров обогнал первый пловец второго к моменту финиша? (Cм. № 468, [12]).

В основном в учебнике обучение выбору точности числовых значений реализуется при построении различных графиков зависимостей.

К этому типу задач относятся также:

5 класс, часть 1, [11]: №№ 330, 345;

5 класс, часть 2, [12]: №№ 111, 112, 129, 179, 548, 592, 638, 649, 890;

6 класс, часть 1, [13]: №№ 55, 77-80, 92, 155, 162, 280, 317, 468, 473;

6 класс, часть 2, [14]: №№ 33, 37, 38, 50, 51,81, 84, 113, 140, 141-144, 154, 155, 173, 175, 176, 178, 189, 190, 265, 288, 374;

6 класс, часть 3, [15]: №№ 146, 155, 158, 198.

Задачи, которые должны использоваться при обучении действию оценки возможности получения результата, представлены в учебнике в небольшом количестве. К ним относятся такие задачи, как:

В классе 20 учеников. Из них английский язык изучают 15 человек, немецкий – 10, и еще 1 человек изучает французский язык. Возможно ли это? (Cм. № 336, [13]).

На туристической карте масштаб оказался оторванным. Можно ли его восстановить, если известно, что расстояние от сельской почты до окраины села (по прямой дороге) равно 3,2 км, а на карте это расстояние изображено отрезком длиной 4 см? (Cм. № 49, [14]).

В городской думе 80 депутатов, среди которых 4 независимых депутата, а остальные представляют интересы трех партий. Число депутатов от первой партии на 20% больше, чем от второй, а число депутатов от второй партии составляет 62,5% числа депутатов третьей. Может ли какая-либо партия заблокировать принятие решения, для которого требуется квалифицированное большинство голосов (не менее 2/3) всех депутатов? (Cм. № 368 (б), [15]).

В процессе решения предложенных и аналогичных задач учащиеся должны усвоить, что выбор точности зависит от цели, с которой решается задача, и от качеств самого измеряемого объекта. При ответах школьники опираются на свои представления о реальных объектах и процессах, описанных в задаче.

Анализ учебников [11], [12], [13], [14], [15] показал, что в них содержится достаточное количество задач для формирования простейших умений, входящих в метод математического моделирования. Кроме того, вводится понятие «математическая модель» и описываются этапы математического моделирования. Школьники учатся оперировать с моделями. Все это создает предпосылки для более осознанного дальнейшего обучения математике.

Опытное преподавание осуществлялось в школе № 21 г. Кирова.

Смотрите также::

Сущность содержательно-оценочной основы обучения
Вся учебно-воспитательная работа с детьми, ее методы, приемы, формы, «пройдя через душу педагога, согретую любовью к детям и наполненную чувством гуманности, становятся утонченными, гибкими, целенаправленными и потому — эффективными», — утверждает Ш.А. Амонашвили. Из этих высказываний определенно в ...

Методические рекомендации родителям по профилактике компьютерной зависимости детей и подростков
Задача параграфа: рассмотреть рекомендации родителям по профилактике компьютерной зависимости школьников. Проанализировать воспитательную деятельность педагога, родителей. Раскрыть этапы профилактики компьютерной зависимости Полученные в результате исследования, данные позволяли нам выработать мето ...

Состояние проблемы
Детство – важнейший период человеческой жизни, это не подготовка к будущей жизни, а настоящая, яркая, самобытная, неповторимая жизнь. И от того как, прошло детство, кто вел ребенка за руку в детские годы, что вошло в его разум и сердце из окружающего мира – от этого в решительной степени зависит, к ...