Математическое моделирование в школе

Получили, что и .

III этап. Интерпретация. Переведем результат с математического языка на язык исходной задачи.

Так скорость автомобиля не может быть отрицательным числом, то условию задачи соответствует только один корень , т.е. скорость второго автомобиля равна 80 км/ч, а скорость первого 90 км/ч.

Задача 2. Группа студентов решила купить магнитофон ценой от 170 до 195 долларов. В последний момент двое отказались участвовать в покупке, поэтому каждому из оставшихся пришлось внести на 1 доллар больше. Сколько стоил магнитофон?

Решение.

I этап. Формализация. Построим математическую модель задачи. Пусть х - число студентов в группе, у долларов – величина первоначально предлагаемого взноса. Тогда стоимость магнитофона . После того, как двое отказались участвовать в покупке, студентов стало , а взнос составил доллар. Следовательно стоимость магнитофона равна . Условие задачи можно представить в виде системы

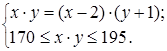
Математическая модель построена.

II этап. Внутримодельное решение. Рассмотрим систему, состоящую из уравнения и неравенства

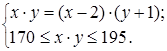
В уравнении раскроем скобки и приведем подобные. Получим следующую систему

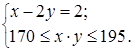
Из уравнения выразим y, . Следовательно, . Так как х - натуральное число, то сейчас систему неравенств можно решать в натуральных числах. Из неравенства имеем х. Из неравенства имеем х. Таким образом, нужно найти натуральные решения неравенств . Ясно, что х = 20. Тогда у = 9 и = 180.

III этап. Интерпретация. Переведем результат с математического языка на язык исходной задачи. Магнитофон стоил 180 долларов.

Задача 3. Окно имеет форму прямоугольника, завершенного сверху полукругом. Укажите такие размеры окна, чтобы при данном периметре l оно пропускало больше света.

Решение.

I этап. Формализация. Построим математическую модель данной задачи.

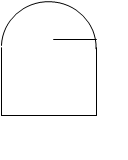Требуется найти размеры окна с наибольшей площадью. Обозначим размеры: r – радиус полукруга, h – высота прямоугольника, тогда основание прямоугольника 2r.

Чтобы определить, какое из переменных выбрать аргументом исследуемой функции, надо посмотреть, какое из них проще выражается через другое:

Смотрите также::

Советская система дошкольного образования
Начало государственной системы дошкольного образования в нашей стране было положено после принятия 20 ноября 1917 года «Декларации по дошкольному воспитанию». В этом документе были определены принципы советского дошкольного образования: бесплатность и доступность общественного воспитания детей дошк ...

Ведущие принципы обучения иноязычному общению дошкольников
Принцип овладения иностранным языком через общение. Процесс обучения иноязычному общению представляет собой модель реального общения по следующим основным параметрам: мотивированность, целенаправленность, информативность процесса общения, новизна, ситуативность, функциональность, характер взаимодей ...

Развитие воображения у младших школьников
У детей третьего года жизни можно наблюдать первые проявления воображения. К этому времени у ребенка накопился уже некоторый жизненный опыт, который дает материал для работы воображения. К концу дошкольного периода детства у ребёнка, чьё творческое воображение развивается достаточно быстро, воображ ...