Математическое моделирование в школе

Третий шаг – это перевод неформальной модели в математическую модель. Такой перевод включает в себя рассмотрение словесного описания неформальной модели и поиск подходящей математической структуры, способной отобразить изучаемые процессы. Это самый сложный этап во всем процессе моделирования. Стадия перевода может таить в себе две опасности. Во-первых, неформальные модели имеют тенденцию быть неоднозначными, и обычно существует несколько способов перевода неформальной модели в математическую (при этом альтернативные математические модели могут иметь совершенно различный смысл). На самом деле это одна из главных причин, изначально толкающих к применению математических моделей: язык математики лишен двусмысленностей и более точен, чем естественный язык, он позволяет исследовать скрытый смысл тончайших различий в формулировках, который плохо доступен исследованию посредством естественного языка.

Следующий этап – этап решения задачи в рамках математической теории – можно еще назвать этапом математической обработки формальной модели. Он является решающим в математическом моделировании. Именно здесь применяется весь арсенал математических методов – логических, алгебраических, геометрических и т. д. – для формального вывода нетривиальных следствий из исходных допущений модели. На стадии математической обработки обычно – вне зависимости от сути задачи – имеют дело с чистыми абстракциями и используют одинаковые математические средства. Этот этап представляет собой дедуктивное ядро моделирования.

На последнем этапе моделирования полученные выводы проходят через еще один процесс перевода – на сей раз с языка математики обратно на естественный язык.

Рассмотрим на примере реализацию всех этапов процесса математического моделирования.

Задача 1. Два автомобиля выехали одновременно из пункта А в пункт В, расстояние между которыми 540 км. Первый автомобиль ехал со скоростью, на 10 км/ч большей, чем второй, и прибыл в пункт В на 45 мин раньше второго. Найдите скорость каждого автомобиля.

I этап. Формализация. Построим математическую модель задачи.

Обозначим за x км/ч – скорость второго автомобиля, тогда скорость первого автомобиля равна (x+10) км/ч.

ч – время, потраченное на весь путь вторым автомобилем.

ч – время, потраченное на весь путь первым автомобилем.

Известно, что второй автомобиль потратил на путь на 45 мин больше, чем первый. .

. Полученное уравнение является математической моделью данной задачи.

II этап. Внутримодельное решение.

Перенесем все слагаемые в одну часть .

Приведем слагаемые к общему знаменателю .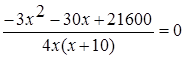

Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю. Получим следующую систему: .

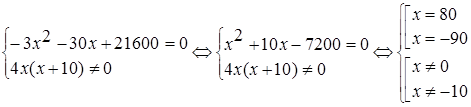Смотрите также::

Этапы формирования просодической стороны речи у детей с нарушением опорно-двигательного аппарата, имеющих речевые нарушения
Методические рекомендации разработаны с целью оказания помощи детям в общении с другими людьми, обучения произвольному и эффективному использованию всех имеющихся в русском языке выразительных средств устной речи. Изучив предложенные методики по формированию просодической стороны речи, мы адаптиров ...

Овладение просодической стороной речи в онтогенезе
Первый год жизни, несмотря на то, что ребенок еще не говорит, является очень важным для формирования речи и всех ее компонентов. Устная речь предполагает наличие голоса, и уже вскоре после рождения крик приобретает различную обертональную окраску в зависимости от состояния ребенка. Крик является пе ...

Психолого-педагогическая характеристика младших школьников с речевыми нарушениями
Дети с речевыми нарушениями обычно имеют функциональные или органические отклонения в состоянии центральной нервной системы [30]. Наличие органического поражения мозга обусловливает то, что эти дети плохо переносят жару, духоту, езду в транспорте, долгое качание на качелях, нередко они жалуются на ...