Математическое моделирование в школе

l=2r+2h+r, h=, r=.

Удобней выбрать r, так как для выражения площади понадобится r2, а h входит в это выражение линейно.

S(r)= 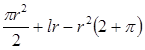. Эта функция и есть модель данной задачи.

II этап. Внутримодельное решение.

Ясно, что 0<r<.

Найдем производную функции S(r): .

Воспользуемся необходимым условием экстремума: l-r(+4)=0. Отсюда r=. Из соображений здравого смысла окно не может иметь наименьшую площадь, поэтому найденное значение r – точка максимума. При этом r=h=.

III этап. Интерпретация. Переведем результат с математического языка на язык исходной задачи. Чтобы при данном периметре l окно пропускало больше света, необходимо установить следующие размеры окна: r=h=

Учителю следует добиться от учащихся четкого понимания значения и содержания каждого из выше описанных этапов процесса математического моделирования. Это нужно для того, чтобы школьники усвоили, что они решают не просто математическую задачу, а конкретную жизненную ситуацию математическими методами. Тогда учащиеся смогут увидеть в математике практическое значение, и не будут воспринимать ее как абстрактную науку.

Метод математического моделирования является мощным инструментом для исследования различных процессов и систем. Приложения этого метода к решению конкретных задач изложены в ряде известных монографий и учебных пособий. Вместе с тем, многие из них предполагают достаточно высокий уровень математической подготовки учеников, что зачастую вызывает определенные трудности при изучении материала. Понятие математической модели и некоторые общие положения, связанные с ним, должны в той или иной форме иллюстрироваться на протяжении всего курса математики, а разделы школьной программы, посвященные задачам на работу, движение, проценты, прогрессии и, наконец, задачам на применение производных и интегралов, могут рассматриваться как введение в метод математического моделирования.

Смотрите также::

Содержательно-технологические аспекты социально-педагогической программы по профилактике компьютерной зависимости детей и подростков
В этом параграфе мы рассмотрим проведенный констатирующий эксперимент, цели, задачи и методы эксперимента. С целью анализа и характеристики состояния уровня компьютерной зависимости был проведен констатирующий эксперимент, который проводился в экспериментальных классах, в 7, 9 и 11 классе, где 75 ч ...

Ценностные аспекты межкультурной коммуникации, как фактор консолидации современного общества в процессе изучения иностранных языков в ВУЗе
По определению А.П. Садохина межкультурная коммуникация – есть совокупность разнообразных форм отношений и общения между индивидами и группами, принадлежащими к разным культурам. Определение межкультурной коммуникации объясняется самим же термином: это общение людей, представляющих разные культуры. ...

Модернизация содержания школьного исторического образования в начале 1960-х - конце 1980-х гг
Период 1960-х - 1980-х гг. характеризуется временем совершенствования теории и практики обучения истории в школе Практика жизни - дальнейшее развитие научно - технической революции(многие авторы считают более приемлемым термин «научно-технический прогресс») в целом мире и в нашей стране в частности ...