Примерные уроки по теме «Прямоугольный треугольник»

– Заметили ли вы какую-нибудь зависимость?

Учащиеся называют свои гипотезы, учитель опровергает их контр примерами.

– Читала я в древних китайских рукописях о каких-то квадратах. Давайте попробуем возвести длины сторон треугольников в квадрат.

Таким образом, получаем правую часть таблицы:

2. Учащиеся выдвигают гипотезу: а2+в2=с2.

– Чем являются a, b и c в нашем треугольнике? Сформулируйте нашу гипотезу с помощью терминов «катет» и «гипотенуза».

3. Доказательство гипотезы.

Как показывает опыт, при доказательстве теоремы Пифагора затруднение у учащихся возникает только в том, чтобы запомнить дополнительное построение. В этом помогает нам рисунок.

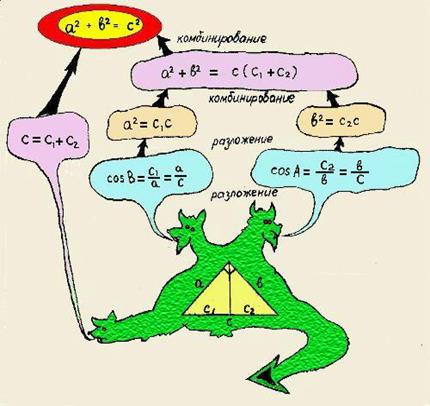
Доказательство начинается так (аналогия со сказкой): отрубили у дракона одну голову («разрубили» треугольник высотой), а у него две выросли. Запомнив этот рисунок, ученик запомнит и дополнительное построение, а дальше восстановит доказательство логическим путем. Рисунок как помощник памяти «действует» в содружестве с логикой одновременно подстраиваясь под живое и непосредственное детское восприятие.

– Обычно открытие этой теоремы приписывают древнегреческому философу и математику Пифагору, поэтому в геометрии она известна под его именем. Давайте ее еще раз сформулируем.

В Древней Индии эту теорему доказывали интересным способом. На этих рисунках видим, что слева свободная от треугольников фигура состоит из двух квадратов со сторонами а и в, соответственно ее площадь равна

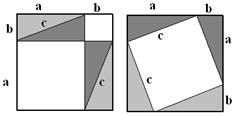
а2+в2, а справа – квадрат со стороной с, его площадь равна с2. Значит а2+в2=с2.

А теперь ответьте на вопрос, поставленный в начале урока: какой длины лестницу мне нужно построить?

А сможем ли мы найти катет, если известны гипотенуза и другой катет?

Закрепление.

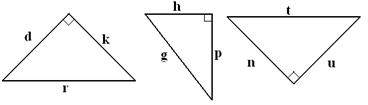
1. Назовите равенство, используя теорему Пифагора.

2. В прямоугольном треугольнике один из катетов равен 6 см, гипотенуза – 4 см. Найдите второй катет.

(При решении этой задачи учащиеся приходят к выводу, что катет не может быть больше гипотенузы.) Исправьте условие задачи.

3. Дан прямоугольный треугольник. Составьте задачу, при решении которой нужно будет воспользоваться теоремой Пифагора. Обменяйтесь задачами с соседом по парте и решите их.

В качестве задания, закрепляющего сформированный частный прием, можно предложить задачу древних индусов, сформулированную в виде стихотворения, взятую из книги Я.И. Перельмана «Занимательная геометрия». Отметим, что эта задача имеет ярко выраженное практическое применение.

Над озером тихим,

С полметра размером,

Смотрите также::

Анализ стандартов по дисциплине «Компьютерные коммуникации и сети» и определение цели обучения
При подготовке будущих специалистов в области информационных технологий одно из главных мест занимает дисциплина «Компьютерные коммуникации и сети». Согласно государственного образовательного стандарта изучение этой дисциплины позволяет сформировать у обучаемого целостное представление об основах, ...

Сущность формирования профессиональных умений и навыков
Движения и действия реализуются у человека сознательно и бессоз-нательно. Осознаются, как правило, конечные цели действий, а также общий их характер. С одной стороны, никакое действие человека не бывает до кон-ца автоматизированным (т. е. удаленным из сознания), потому что оно в конечном счете вызы ...

Организация социальной работы по формированию здорового образа жизни у подростков
Зарубежные исследования показали, что после первоначального эффекта, произведенного новой информацией, она уже не играет значительной роли. Так, например, программы борьбы с курением, созданные исключительно в когнитивном ключе, почти не оказывают влияния на подростков. Сегодня любой из них запрост ...