Примерные уроки по теме «Прямоугольный треугольник»

AB = 18, AB = 12 см; AC = 18 – 12 = 6 см.

Ответ: AB = 12 см, AC = 6 см.

3. Решить задачу №260.

Задача. Высота, проведённая к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторона треугольника равна 15,2 см. Найдите у4глы этого треугольника.

Решение. Дан треугольник DMC; DM = MC; MO┴DC; DM = 15,2 см; MO = 7,6 см. Найти углы треугольника DMC.

Так как MO = DM, то по свойству 3º < D = 30º, тогда < C = 30º,

< M = 180º – (30º + 30º) = 180º – 60º = 120º.

Ответ: < D = < C = 30º; < M = 120º.

III. Итоги урока.

Домашнее задание: изучить пункт 34 учебника о некоторых свойствах прямоугольного треугольника; повторить пункты 15 – 33, связанные с признаками равенства треугольников. Ответить на вопросы 10 и 11 на стр. 84; решить №256, 259.

Урок 2. Признаки равенства прямоугольных треугольников

Цели: доказать признаки равенства прямоугольных треугольников и показать, как они применяются при решении задач.

Ход урока

I. Повторение изученного материала.

1. Сформулировать свойства прямоугольных треугольников.

2. Вспомнить признаки равенства треугольников.

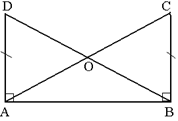
3. Решить задачу: гипотенузы BD и AC прямоугольных треугольников ABD и ABC с общим катетом AB и с равными катетами AD и BC пересекаются в точке O. Докажите, что треугольник AOB равнобедренный.

II. Изучение нового материала.

1. Учащиеся самостоятельно (устно), используя признаки равенства треугольников, доказывают признаки равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу (учитель держит перед классом два равных прямоугольных треугольника и задаёт наводящие вопросы).

2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу (устно) по моделям равных прямоугольных треугольников.

3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету проводит сам учитель (используя рисунок учебника), так как доказательство этого признака требует дополнительных построений и непростых логических рассуждений.

III. Закрепление изученного материла.

1. Решить задачу №261 на доске и в тетрадях.

Задача. Докажите, что в равнобедренном треугольнике две высоты, проведённые из вершин основания, равны.

Доказательство. Дан треугольник ABC; AD = DC, AB и CK – высоты. Доказать AB = CK.

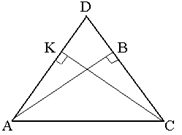
По условию AB ┴DC и CK┴AD, тогда треугольники ABC и AKC – прямоугольные; в них AC – общая гипотенуза и < KAC = < BCA, так как по условию треугольник ADC равнобедренный.

Значит, треугольники ABC и CKA равны (по гипотенузе и острому углу).

Тогда AB =CK.

2. Учащиеся самостоятельно формулируют и доказывают признак равенства прямоугольных треугольников по катету и противолежащему углу (задача №268).

3. Решить задачу №269 на доске и в тетрадях.

Указание: при решении задачи применить вывод задачи №268 – признак равенства прямоугольных треугольников по катету и противолежащему углу.

IV. Итоги урока.

Домашнее задание: изучить пункт 35; ответить на вопросы 12, 13 на стр. 84; решить задачи №262, 264.

Урок 3. Решение задач

Цели: научить применять признаки равенства прямоугольных треугольников и их свойства при решении задач; вырабатывать умение решать задачи; учить логически мыслить.

Смотрите также::

Виды воображения
Воображение может функционировать на различных уровнях. Различие их определяется прежде всего тем, насколько активно, сознательно относится человек к этому процессу. По степени выраженности активности различают два вида воображения: пассивное и активное. Для пассивного воображения характерно создан ...

Сущность педагогического мастерства
Воплощение педагогического искусства в жизнь невозможно без овладения воспитателем педагогическим мастерством, техникой и технологией педагогического действия. Мастерство материализуется в умениях и навыках, через овладение способами и приемами педагогического труда. Они становятся неотъемлемой час ...

Особенности танцевальной деятельности детей 6-7 лет
Анализ психолого-педагогической литературы и опыт учителей-практиков, музыкальных работников, психологов, врачей позволяет утверждать, что развитие танцевальных на каждом возрастном этапе происходит различно. В младшем возрасте ребенок эмоционально откликается на музыку, что выражается в мимике, же ...