Методические рекомендации к изучению темы «Прямоугольный треугольник»

Проблемы, которые учитель может ставить перед учениками, обычно разрешаются на протяжении одного или нескольких уроков.

Наиболее часто учителя создают проблемные ситуации при помощи эксперимента, то есть исследования частного случая.

Легко организовать проблемную ситуацию, предложив ученикам задачи, для решения которых нужны новые знания. Полезно при этом поддерживать накал активности цепью проблемных вопросов, сменяющих один другой.

Перед изучением теоремы Пифагора рассматривается практическая задача, для решения которой нужно уметь вычислить длину гипотенузы по длинам катетов.

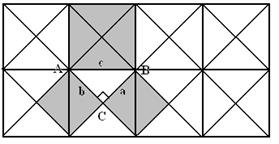
Построение убеждает, что определенная зависимость между катетами и гипотенузой существует, что два катета определяют треугольник, в котором гипотенуза не может быть произвольной. Можно найти приблизительное решение графическим путем. Теперь возникает вопрос: «Можно ли выразить формулой зависимость между катетами и гипотенузой?». В поисках ответа рассмотрим удобный частный случай: прямоугольный треугольник с острыми углами по 45º.

Получаем для него формулу

c2 = a2 + b2 и задаёмся вопросом: «Верна ли эта формула для произвольного прямоугольного треугольника?».

Дальнейшее исследование может быть построено по такой схеме. Поскольку в предлагаемую формулу входят величины a2, b2, c2, то есть площади квадратов со сторонами a, b, c. Построим эти квадраты. Первое построение («пифагоровы штаны») идею доказательства не поясняет.

Тогда учитель предлагает связать величины a, b и c в комбинации прямоугольных треугольников и квадратов таким образом, каким показано на рисунке.

Рассмотрим данный рисунок. Понятно, что с одной стороны площадь большого квадрата равна произведению двух сторон, которые выражены как (a+b). Отсюда следует, что площадь равна (a+b)2.

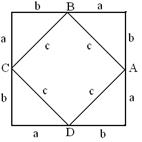
С другой стороны площадь большого квадрата равна сумме площадей фигур, на которые разбит данный квадрат. В данном случае, это сумма малого квадрата со стороной c и четырёх равных треугольников со сторонами a, b и c.

Отсюда следует, что площадь малого квадрата равна разности площади большого квадрата со стороной (a+b) и учетверённой площади треугольника со сторонами a, b и c, то есть

c2 = (a + b)2 –

c2 = a2 + 2ab + b2 –

2c2 = 2a2 + 4ab + 2b2 – 4ab

2c2 = 2a2 + 2b2

c2 = a2 + b2

Можно ли считать формулу доказанной? Если исходить из такой формулы, которая дана на чертеже, то да. Рассмотрим, всегда ли можно для любого прямоугольного треугольника провести такое построение. Строим квадрат со стороной (a + b) и строим прямоугольный треугольник с катетами a и b. Выясним, почему все такие треугольники равны. Остаётся показать, что фигура, образованная гипотенузой и полученных прямоугольных треугольников, является квадратом. Замечаем, что все стороны этой фигуры равны как гипотенузы равных треугольников. Но достаточно ли этого, чтобы фигура ABCD была квадратом? – Нет. Доказываем, что все углы этой фигуры прямые, так как они равны разности развёрнутого угла и острых углов данного прямоугольного треугольника. Следовательно, теорему Пифагора можно считать доказанной.

В качестве домашнего задания учитель может поручить ознакомиться с доказательством, данным в учебнике.

Смотрите также::

Понятие и сущность познавательной деятельности дошкольника
Познавательная деятельность - это специфический вид активности человека, направленный на познание и творческое преобразование окружающего мира, включая самого себя и условия своего существования. В деятельности человек создает предметы материальной и духовной культуры, преобразует свои способности, ...

Государственные, отраслевые стандарты образования и стандарты ВУЗ
Министерство образования и науки Украины вынесло на общественное обсуждение новую редакцию закона Украины "О высшем образовании". Законопроект подготовлен с целью приведения законодательства Украины в сфере высшего образования к требованиям Болонского процесса, к которому Украина присоеди ...

Определение понятия педагогического эксперимента
Существует множество определений понятия "педагогический эксперимент". Педагогический эксперимент - это метод познания, с помощью которого исследуются педагогические явления, факты, опыт. Педагогический эксперимент - это специальная организация педагогической деятельности учителей и учащи ...