Методические рекомендации к изучению темы «Прямоугольный треугольник»

Утверждения об углах прямоугольного треугольника, являясь прямыми следствиями из теоремы о сумме углов треугольника, чрезвычайно просто доказываются. Их доказательства можно предложить провести учащимся самостоятельно.

Один из углов прямоугольного треугольника равен: а) 20º; б) 30º; в) 45º. Найти второй острый угол треугольника.

Определите острые углы прямоугольного треугольника, если один из них в 2 раза больше другого.

Далее рассмотреть свойства прямоугольного треугольника. Изучение пункта 34 о свойствах прямоугольного треугольника» можно начать с решения задачи 254 и 255. После этого рассмотреть свойство 1, которому следует уделить особое внимание (катет прямоугольного треугольника, лежащего против угла в 30º, в два раза меньше гипотенузы). Так как учащиеся будут использовать его при решении задач, а в дальнейшем – при получении значений тригонометрических функций углов 30° и 60°. Использование этого свойства можно показать на примере задачи 265. Доказательство свойств 2 и 3 следует провести учителю самому с записью условия и заключения прямого и обратного утверждений на доске в виде таблицы. Эту таблицу учащиеся должны воспроизвести в своих тетрадях.

Затем рекомендуется решить задачи 257, 259, 260.

Перед доказательством специальных признаков равенства треугольников полезно вспомнить общие признаки, но не отвлечённо, применительно к прямоугольным треугольникам. Это можно сделать, предложив, например, устно по готовому рисунку провести доказательства:

1. Докажите, что если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то такие треугольники равны.

2. Докажите, что два прямоугольных треугольника ABC и A1B1C1 с прямым углом C и C1 равны, если у них равны катеты BC B1C1 и прилежащие к ним острые углы: <B и <B1.

После выполнения задачи 2 можно сделать замечание о том, что если в прямоугольных треугольниках ABC и A1B1C1 <A = <A1, то и <B = <B1, так как углы B B1 дополняют до 90º равные углы A и A1. А значит, можно доказать равенство этих треугольников по катету и противолежащему острому углу.

Следует также сказать, что этот признак и ещё два признака, которые могут рассматриваться далее, являются специальными признаками прямоугольных треугольников.

Доказательство этого признака можно предложить учащимся провесит самостоятельно.

Сформулировать признак равенства прямоугольных треугольников по гипотенузе и острому углу, учитель может и его предложить учащимся доказать самостоятельно.

Закрепить доказанные признаки можно а ходе выполнения заданий.

Обоснуйте равенство треугольников на рисунке а).

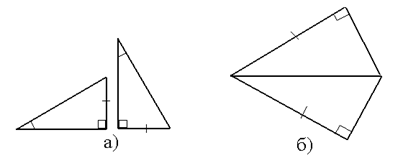
2. На рисунке б) <B = <D = 90º, BC║AD. Докажите, что ΔABC = ΔCDA.

Или решить задачи 261,263 из учебника.

Смотрите также::

Педагогические условия развития коммуникативных способностей первоклассников в процессе образования
В данном параграфе нами были рассмотрены педагогические условия развития коммуникативных способностей первоклассников в процессе образования. Согласно гипотезе нашего исследования, а также результатам теоретической разработки проблемы развития коммуникативных способностей первоклассников в процессе ...

Британские традиции семейного воспитания
Таким, как описано выше, представляли себе джентльмена в обществе, породившем это понятие. Какие же требования к джентльмену сохранились к началу нашего столетия? В определении понятия "джентльмен" поначалу на первом месте стоит происхождение, генеалогическое древо, право на имение герба. ...

Сценическое действие эстрадного искусства
По мере своего развития театр сформировался как вид искусства, отображающего действительность в динамических и протяженных формах самой жизни, а концертное исполнительство осталось в основном искусством рассказа (словесного, музыкального, пластического) об отдельных ее моментах. Для создания наибол ...