Два подхода к решению прямоугольных треугольников

Существует два подхода к изложению темы «Решение прямоугольных треугольников».

Первый подход основан на запоминании четырёх определений основных тригонометрических функций и ещё шести правил:

1. Катет равен гипотенузе, умноженной на синус противолежащего угла;

2. Катет равен гипотенузе, умноженной на косинус прилежащего угла;

3. Катет равен другому катету, умноженному на тангенс противолежащего угла;

4. Катет равен другому катету, умноженному на котангенс прилежащего угла;

5. Гипотенуза равна катету, делённому на синус противолежащего угла;

6. Гипотенуза равна катету, делённому на косинус прилежащего угла.

Второй подход, в отличие от первого, вынуждает учащихся запомнить лишь четыре определения тригонометрической функции острого угла. Это ведёт к меньшей нагрузке на память. Однако и здесь таятся некоторые трудности для учащихся. Они связаны, во-первых, с выбором нужной функции в условиях конкретной задачи, а во-вторых, с тем, что использование их определений не даёт непосредственного знания нужного элемента треугольника, а лишь приводит к уравнению, из которого этот элемент надо найти. Например:

tg α =, x=, x=ctg α.

Этих трудностей можно избежать, если ввести понятие единичного прямоугольного треугольника.

Назовём этим термином прямоугольный треугольник с гипотенузой, равной единице.

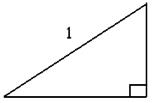
В дальнейшем будем называть его просто единичным треугольником. Пусть один из его острых углов равен α. Тогда очевидно, что длина его противоположного катета равна sin α, а прилежащего – cosα.

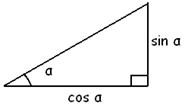
Эти сведения ученик должен запомнить, что, в общем-то, несложно, так как всегда синус ассоциируется с противолежащим катетом, а косинус с

прилежащим катетом. Кстати, такой подход обнаруживает эффективный способ вычисления синуса, косинуса и служит пропедевтикой к их определению с помощью единичной окружности.

Пусть теперь дан произвольный прямоугольный треугольник со сторонами k, l, m и острым углом α. Наряду с ним рассмотрим единичный треугольник с таким же углом α. Ясно, что единичный треугольник (пусть длины его сторон равны соответственно k1, l1, m1) подобен данному.

Тогда k: l = k1: l1, k=l (1).

Получено правило нахождения любой стороны прямоугольного треугольника. Сформулируем его следующим образом:

Любая сторона прямоугольного треугольника равна другой стороне, умноженной на отношение сходственных сторон единичного треугольника.

Это правило вобрало в себя все шесть правил, приведенных в начале. Оно легко для запоминания, в нем даже не упоминаются термины: «катет», «гипотенуза», «прилежащие и противолежащие катеты», «синус, косинус, тангенс угла». Ученик не стоит перед необходимостью выбора какого-либо правила, формулы и т.д.

Пример. Пусть дан треугольник, у которого катет равен x, а гипотенуза равна a.

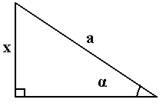
Соответствие сходственных сторон этого треугольника и единичного обозначим стрелками.

xsinα, a1.

Тогда x=a=.

Смотрите также::

Воспитание сказками Пушкина
Пушкин в своих сказках называет чувства. Проведя некоторое исследование, мы убедились, что современные "дети не знают названия чувств"; "Из богатой палитры чувств они в основном замечают крайние: любовь - ненависть, радость - горе". А ведь есть жалость, сочувствие, зависть и т.д ...

Тренажер, включающий модель, основанную на уравнениях баланса с коэффициентами, полученными из экспериментальных данных
Существенным шагом вперед в сфере построения моделей энергоблоков стало признание того факта, что модели должны напрямую строиться на основе физических законов, которыми определяется функционирование реального объекта. Прежде всего, это законы сохранения энергии (тепла), массы и количества движения ...

Выявление характера познавательных интересов учащихся
Развитие познавательных интересов у школьников-подростков имеет большое значение. Подростковый возраст обычно называют переходным, так как в этот период происходит переход от детства к юности. У учащихся этого возрастного периода как бы переплетаются черты детства и черты, во многом присущие юности ...