Углы в прямоугольном треугольнике

30°, 45° И 60°

Найдём сначала значение синуса, косинуса и тангенса для углов 30° и 60°. Для этого рассмотрим прямоугольный треугольник ABC с прямым углом C, у которого < A =30°, <B = 60° (рис. 13).

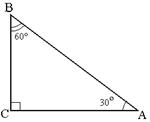
Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то . Но . С другой стороны . Итак, .

Из основного тригонометрического тождества получаем

, .

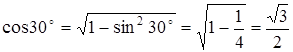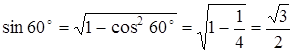По формуле (4) П. 5.1. находим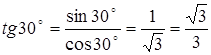

.

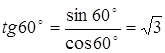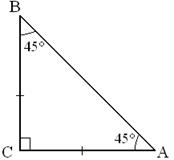
Найдём теперь sin45°, cos45° и tg45°. Для этого рассмотрим равнобедренный прямоугольный треугольник ABC с прямым углом C (рис. 14).

В этом треугольнике AC = BC, < A = < B = 45°. По теореме Пифагора

AB2 = AC2 + BC2 = 2AC2 = 2BC2, откуда AC = BC =. Следовательно,

.

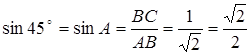
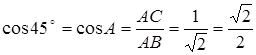
Составим таблицу значений sinα, cosα, tgα для углов α, равных 30°, 45°, 60°.

урок геометрия треугольник теорема

Смотрите также::

Пути формирования познавательного интереса у учащихся и развитие их творческих способностей
Существует множество различных методов формирования интереса учащихся к учебному предмету. Одним из методов является организация межпредметных связей на уроке. Этот метод имеет двухстороннюю направленность. С одной стороны, учащиеся, интересующиеся физикой, должны проявлять интерес и к другим предм ...

Функции и цели обучения математическому моделированию в школе
Терешин Н. А. выделяет следующие дидактические функции ма­тематического моделирования: Познавательная функция. Методической целью этой функции является формирование познавательного образа изучаемого объек­та. Это формирование происходит постоянно при переходе от просто­го к сложному. Здесь мысль уч ...

Использование метода беседы для развития самостоятельности учащихся на уроках ботаники в v классе
лабораторный практикум ботаника самостоятельный беседа Применению метода беседы в учебном процессе уделяли внимание многие дидакты и методисты. В помощь учителю приводились рекомендации по составлению и постановке вопросов беседы, ходу логических рассуждений. Давалась и классификация беседы: вводна ...