Углы в прямоугольном треугольнике

Синус, косинус и тангенс острого угла в прямоугольном треугольнике

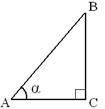
Рассмотрим прямоугольный треугольник ABC с прямым углом C (рис. 10). Катет BC этого треугольника является противоположным углу A,

а катет AC – прилежащим к этому углу.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Синус, косинус и тангенс угла равного α обозначается символами sin α, cos α и tg α (читается: «синус альфа», «косинус альфа» и «тангенс альфа»). На рисунке

, (1)

, (2)

, (3)

Из формул (1) и (2) получаем: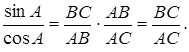

Сравнивая с формулой (3), находим

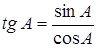(4),

то есть тангенс угла равен отношению синуса к косинусу этого угла.

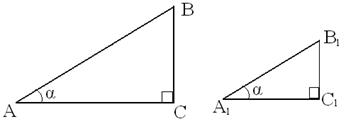
Теорема. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

Доказательство. Пусть ABC и A1B1C1 – два прямоугольных треугольника с прямыми углами C и C1 и с одним и тем же углом при вершине A и A1 равны α (рис. 11).

Треугольники ABC и A1B1C1 подобны по первому признаку подобия треугольников, поэтому 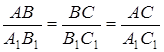. Из этих равенств следует, что 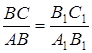, то есть .

Аналогично 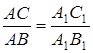, то есть , и 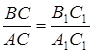, то есть .

Что и требовалось доказать.

Докажем теперь справедливость равенства

(5).

Из формул (1) и (2) получаем . По теореме Пифагора , поэтому .

Равенство (5) называется основным тригонометрическим тождеством.

Представим ещё одно доказательство теоремы Пифагора, основанное на определении косинуса угла в прямоугольном треугольнике.

Доказательство. Пусть ABC – данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C. (рис. 12).

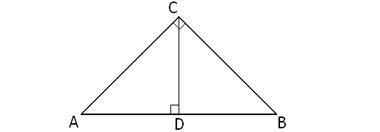
По определению косинуса угла . Отсюда . Аналогично . Отсюда .

Складывая полученные равенства почленно, и, замечая, что AD+DB=AB, получим .

Что и требовалось доказать.

Значение синуса, косинуса и тангенса для углов

Смотрите также::

Программа работы социального педагога по профилактике виктимности подростков
Изучив научную литературу по проблеме виктимности подростков, считаем целесообразным, чтобы работа социального педагога в этом направлении носила не только профилактический, но и развивающий характер. Статистические данные об авариях на дорогах, росте наркомании, отравлении алкоголем, гибели людей ...

Виды эмоций
Значение собственно эмоций в эмоциональной жизни человека особенно велико. Оно состоит в следующем. Во-первых, они являются основой развития чувств. Чувство возникает и развивается путем обобщения эмоций, возникающих к объекту в разных ситуациях. Во-вторых, эмоции «запускают» то или иное настроение ...

Методика применения ТСО
№ Название Назначения Недостатки Применение 1 Плакаты и макеты, статичные и действующие Иллюстрация, включение зрения в процесс усвоения Неэффективность при изучении и взаимосвязи, ограниченность показа В качестве наглядной иллюстрации при изучении и контроле несложных процессов и явлений 2 Эпидиас ...