Признаки равенства прямоугольных треугольников

Чтобы установить равенство прямоугольных треугольников, достаточно знать, что два элемента одного треугольника соответственно равны двум элементам другого треугольника (исключая прямой угол). Это, конечно, не распространяется на равенство двух углов одного треугольника двум углам другого треугольника.

Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис 5).

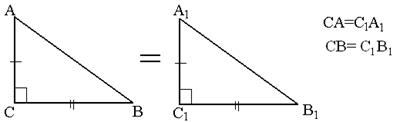
Далее, из второго признака равенства треугольников следует:

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого треугольника, то такие треугольники равны (рис. 6).

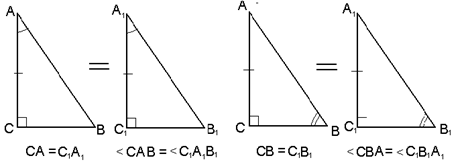
Рассмотрим ещё два признака равенства прямоугольных треугольников.

Теорема. Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 7).

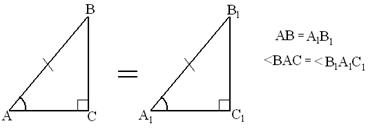
Доказательство. Из свойства 1º §2 следует, что в таких треугольниках два других острых угла тоже равны, поэтому треугольники равны по второму признаку равенства треугольников, то есть по стороне (гипотенузе) и двум прилежащим углам.

Что и требовалось доказать.

Теорема. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых углы C и C1 – прямые, AB =A1B1, BC = B1C1 (рис. 8).

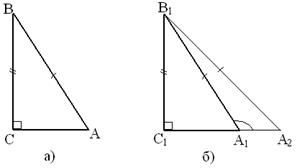
Так как < C = < C1, то треугольник ABC можно наложить на треугольник A1B1C1 так, что вершина C совместится с вершиной C1, а стороны CA и CB наложатся соответственно на лучи C1A1 и C1B1, поскольку CB = C1B1, то вершина B совместится с вершиной B1. Но тогда вершины A и A1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A2 луча C1A1, то получим равнобедренный треугольник A1B1A2, в котором углы при основании A1A2 не равны (на рисунке < A2 – острый, а < A1 - тупой как смежный с острым углом B1A1C1). Но это невозможно, поэтому вершины A и A1 совместятся. Следовательно, полностью совместятся треугольники ABC A1B1C1, то есть они равны.

Что и требовалось доказать.

Смотрите также::

Принцип сознательности и активности
Результативность педагогического процесса во многом определяется тем, насколько сознательно и активно относятся к делу сами воспитываемые. Понимание существа заданий, как и активно заинтересованное выполнение их, ускоряет ход обучения, способствует результативности совершаемых действий, обуславлива ...

Роль внеклассного чтения, как одного из видов внеклассной работы по литературе в личностном развитии школьников
Как известно, любое дело, в том числе и обучение детей чтению, принесёт больше плодов, если оно вызывает интерес. «Учиться надо весело, учиться будем весело, чтоб хорошо учиться». Только живое, эмоциональное, разнообразное по своим приёмам ведение уроков внеклассного чтения привлекает и удерживает ...

Особенности организации детского творческого коллектива
Вообще мир музыкальных звуков окружает ребенка с момента его рождения (например, колыбельные песни) и на протяжении всего периода взросления. Организация детского творческого коллектива - в данное время является очень сложным процессом. Особенно из детей подросткового возраста. Сейчас очень мало лю ...