Подобие прямоугольных треугольников

В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например, футбольный и теннисный мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Введём понятие подобных треугольников.

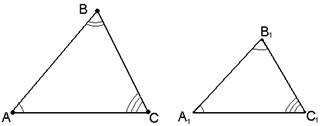
Пусть у двух треугольников ABC и A1B1C1 углы соответственно равны: <A=<A1, <B=<B1, <C=<C1. В этом случае стороны AB и A1B1, BC и B1C1, CA и C1A1 называются сходственными.

Два треугольника называются подобными, если их углы равны и стороны одного треугольника пропорциональны сходственным сторонам другого (рис. 15).

Другими словами, два треугольника подобны, если для них можно ввести обозначения ABC и A1B1C1 так что

<A=<A1, <B=<B1, <C=<C1, (1)

(2).

Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. Обозначается ∆ABC~∆A1B1C1.

Оказывается, что подобие треугольников можно устанавливать, проверив только некоторые из равенств (1) и (2).

У прямоугольного треугольника один угол прямой. Поэтому для подобия прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.

С помощью этого признака подобия прямоугольных треугольников докажем некоторые соотношения в треугольниках.

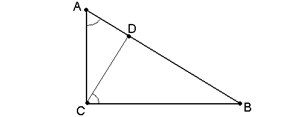
Пусть ABC – прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла (рис. 16).

Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет его на подобные прямоугольные треугольники, каждый из которых подобен данному треугольнику.

На рисунке ABC – прямоугольный треугольник <ABC=90º, CD ┴AB.

Δ ACD ~ Δ CDB;

Δ ACD ~ Δ ABC;

Δ CDB ~ Δ ABC.

Треугольники ABC и CBD имеют общий угол при вершине B. Следовательно, они подобны ∆ABC~∆ CBD. Из подобия треугольников следует пропорциональность соответствующих сторон:

, или , а отсюда следует, что . Это соотношение обычно формулируется так: катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Прямоугольные треугольники ACD и CBD также подобны. У них равные острые углы при вершинах A и C. Из подобия этих треугольников следует пропорциональность их сторон:

или , а отсюда следует, что . Это соотношение обычно формулируется так: высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.

Смотрите также::

Связь педагогики с другими науками
Педагогика, являясь самостоятельной и достаточно научной дисциплиной, не может развиваться обособленно от других наук. Современный этап развития педагогического знания (вторая половина XX в. - начало XXI в.) основан на саморазвитии научной отрасли, сочетающей процессы интеграции и дифференциации с ...

Режиссерский сценарий
Интерактивная игра начинается с заставки, которая призвана произвести на пользователя, в данном случае – ребенка, определенное впечатление, создать настроение и заинтересовать его. Это первое впечатление самое важное. С заставки ребенок должен вникнуть в общий смысл игры. В процессе работы над прое ...

Технология проектной деятельности школьников
Сущность этого типа технологии заключается в личностно-ориентированном обучении, предполагающем развитие личности, способной самостоятельно добывать информацию, принимать нестандартные решения, находить пути решения локальных, региональных и даже глобальных проблем современного развития цивилизации ...