Теорема Пифагора

Значение её состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Одна из теорем позволяет убедиться в том, что если из точки вне прямой проведены к ней перпендикуляр и наклонные, то: а) наклонные равны, если равны их проекции; б) та наклонная больше, которая имеет большую проекцию.

Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия («тригон» – по-гречески означает «треугольник»). Эта наука нашла применение в землемерии. Но еще раньше с ее помощью научились измерять воображаемые треугольники на небе, вершинами которых были звезды. Сейчас тригонометрию применяют даже для измерения расстояний между космическими кораблями.

Пользуясь свойствами площадей многоугольников, мы установим теперь замечательное соотношение между гипотенузой и катетами прямоугольного треугольника. Теорема, которую мы докажем, называется теоремой Пифагора, которая является важнейшей теоремой геометрии.

Если дан нам треугольник,

И при том с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим

И таким простым путем

К результату мы придем.

Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

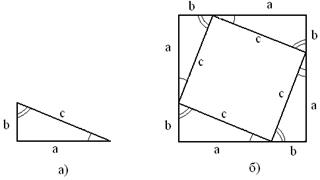
Доказательство. Рассмотрим прямоугольный треугольник с катетами a, b и c (рис. 9 а).

Докажем, что c2 = a2 + b2. Достроим треугольник до квадрата со стороной a+b, так как показано на рисунке (рис. 9 б).

Площадь такого квадрата со стороной a + b равна (a + b)2. С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь которых равна ab, и квадрат со стороной с, поэтому

.

Таким образом, (a + b)2 =2ab + c2, откуда c2 = a2 + b2.

Что и требовалось доказать.

Следствие 1. В прямоугольном треугольнике любой из катетов меньше гипотенузы.

Доказательство. По теореме Пифагора АВ2 = АС2 + ВС2. Так как ВС2>0, то АС2<АВ, То есть АС<АВ.

Следствие 2. Для любого острого угла α cosα <1.

Докзательсво. По определению косинуса cosα = . Но в следствии 1 было доказано, что АС<АВ, значит, дробь меньше 1.

Прямоугольные треугольники, у которых стороны выражаются целыми числами, называются пифагоровыми треугольниками.

Можно доказать, что катеты a, b и гипотенуза c таких треугольников выражаются формулами a=2kmn; b=k(m2-n2); c=k(m2+n2), где k, m и n – натуральные числа, такие, что m>n. Треугольники, со сторонами, длины которых равны 3, 4, 5 называются египетскими треугольниками, т. к. они были известны ещё древним египтянам.

Обратная к теореме Пифагора.

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный (признак прямоугольного треугольника).

Доказательство.

Пусть в треугольнике ABC AB2 = AC2 + BC2. Докажем, что угол C – прямой. Рассмотрим прямоугольный треугольник A1B1C1 с прямым углом C1, у которого A1C1 = AC и B1C1 = BC. По теореме Пифагора A1B12=A1C12+B1C12, и значит, A1B12 = AC2 +BC2. Но AC2 + BC2 = AB2 по условию теоремы. Следовательно, A1B12 = AB2, откуда A1B1 = AB. Треугольники ABC и A1B1C1 равны по трём сторонам, поэтому < C = < C1, то есть треугольник ABC прямоугольный с прямым углом C.

Смотрите также::

Взгляды на воспитание джентльмена в письмах Ф. Честерфилда
В XVIII—XIX вв. огромной популярностью пользовалась книга Ф. Честерфилда "Письма к сыну", не предназначавшаяся автором к печати и изданная после смерти автора. Филипп Стэнхоп, граф Честерфилд, был государственным деятелем, философом, историком, оратором, публицистом. От случайной связи с ...

Понятие об обучении
Обычно обучение характеризуют так: это передача человеку определенных знаний, умений и навыков. Знания, умения и навыки—это формы и результаты определенных процессов в психике человека. Значит, они могут возникнуть в голове чело-века только в результате его собственной деятельности. Их нельзя прост ...

Становление и развитие теоретических знаний в истории православной педагогической культуры России
Приняв Крещение, русский народ получил богатейшую литературу, и прежде всего Библию. В большинстве православных семей России принято было ежедневно читать Евангелие, а Псалтырь знали наизусть, она была практически настольной книгой наших предков. Читая их, человек Древней Руси постигал сущность хри ...