Прямоугольный треугольник и его свойства

Рассмотрим свойства прямоугольных треугольников, которые устанавливаются с помощью теоремы о сумме углов треугольника.

В прямоугольном треугольнике гипотенуза больше катета (следствие из теоремы о соотношении между сторонами и углами в треугольнике).

1°. Сумма двух острых углов прямоугольного треугольника равна 90°.

В самом деле, сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника равна 90°.

2°. Катет прямоугольного треугольника, лежащего против угла в 30º, равен половине гипотенузы.

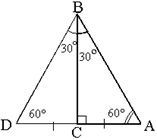
Пусть ABC – прямоугольный треугольник с прямым углом C и углом B равным 30º, а значит, угол A равен 60° (рис. 3). Построим треугольник DBC равный треугольнику ABC, как показано на рисунке. У треугольника ABD все углы равны (60º), поэтому он равносторонний.

Так как AC=AD, а AD=AB, то AC=AB.

Что и требовалось доказать.

3°. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º (обратная теорема).

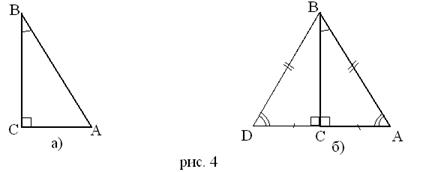
Рассмотрим прямоугольный треугольник ABC, у которого катет AC равен половине гипотенузы AC (рис. 4 а). Докажем, что <ABC = 30°.

Приложим к треугольнику ABC равный ему треугольник DBC так, как показано на рисунке 4 б). Получим равносторонний треугольник DBA. Углы равностороннего треугольника равны друг другу, поэтому каждый из них равен 60°. В частности < DBA=60°. Но <DBA=2<ABC. Следовательно, <ABC=30°.

Что и требовалось доказать.

Смотрите также::

Сценарий уроков по романам писателей-фантастов
Автор: Колесова Инна Константиновна, зам. директора по УМР, учитель русского языка и литературы. Среди многих тем программы 5 класса особый интерес вызывает изучение произведений, представляющих жанр фантастики («научной» и «ненаучной»). Дети читают такие произведения охотно. Можно воспользоваться ...

Методы профессиональной ориентации
В профессиональной ориентации молодежи используются разнообразные методы: информационные, просветительские, экскурсии на предприятия, просмотр фильмов и передач, встречи со специалистами, чтение лекций, профориентационные уроки и т.п. – такие методы называются информационно-справочные. Но поподробн ...

Диагностика сформированности фонематического слуха у детей со стертой дизартрией
Данная система обследования фонематического слуха включает традиционные для логопедической практики приемы для оценки речи детей. Система носит тестовый характер, процедура ее проведения и система балльной оценки стандартизированы, что позволяет наглядно представлять картину дефекта и определить ст ...